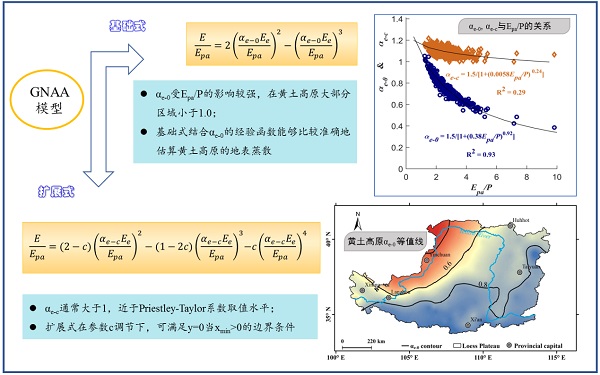
地表蒸散,也称为蒸散发,或者笼统地称为蒸发,是联接水量平衡与能量平衡的纽带,也是水资源消耗的主要形式。2015年美国工程院W. Brutsaert院士基于四个具有物理意义的边界条件,在蒸散估算的平流干旱(AA)模型的基础上提出了更具普遍意义的广义非线性平流干旱(GNAA)模型,把互补蒸散理论研究向前推进了一大步。GNAA模型包括只有一个参数αe-0的基础式与有两个参数αe-c和c的扩展式,其中αe-0和α e-c与著名的Priestley-Taylor公式参数α的位置相当。 GNAA基础式在得到广泛应用的同时,人们发现参数α e-0在不少情况下取值小于1,这与学界普遍接受的Priestley-Taylor参数α需要大于1的认识相悖。藉由黄土高原10个流域长时间序列年尺度水量平衡数据,本项研究发现参数α e-0和αe-c在体现Priestley-Taylor参数α意义的同时,也受到包括干燥指数(Epa/P)在内的多因素的影响,其中以干燥指数的影响最为突出。干燥指数对参数α的影响在GNAA基础式中表现较强,而在扩展式中表现较弱,其结果是基础式中αe-0多有小于1的情况出现,成为Priestley-Taylor参数α的弱的模拟量;而扩展式中由于参数c 的参与,αe-c一般大于1,其在黄土高原的均值为1.08,与Priestley-Taylor参数α的取值水平相当。通过对扩展式中参数c的优化调节,可实现xmin大于0(在y=0时)的边界要求。在地表实际蒸散的估算方面,GNAA基础式结合参数αe-0的经验函数得到的结果精度较高,与此同时论文给出了黄土高原αe-0的等值线分布图。 GNAA基础式和扩展式相结合可以较好地估算地表蒸散,说明参数αe-0和αe-c的取值特征,解释实际蒸散、表观潜在蒸散和潜在蒸散之间的相互关系。
本项研究得到国家自然科学基金项目(41971049)和国家重点研发计划课题(2016YFC0501602)的支持。